A COVID-19 Modeling Story

This is a retrospective post that I wrote some time ago, but never finalized.

Early in 2020, I was working with a healthcare organization that owned hospitals, clinics, and a health insurance company. I was asked by a colleague whether I thought this new disease coming out of China, called COVID-19, was a concern. At the time, I said that the flu season appeared to be more of a concern since it had been rather bad. Supporting this point of view and providing a source of personal bias, I had a very bad upper respiratory infection in Dec 2019 that lasted for weeks. Like many people, especially in the United States, I was very wrong about COVID-19

Once it became apparent that the spread of the virus SARS-CoV-2 was out of control in the US, I was pulled into a small team dedicated to providing the organization with predictive modeling of the COVID-19 hospital admissions, ICU beds, and ventilator usage. The team consisted of a statistician (PhD), an epidemiologist (PhD), an operations researcher / industrial engineer (PhD and masters, respectively), and me (bachelor's degree in psychology). The statistician was the only individual in the entire organization with the title "Data Scientist". My title at the time was "Senior Healthcare Analyst", and I barely had any qualifications to be included on this team. If I guessed as to why I was selected, I would say: 1) I'm a creative problem solver and pretty good at automation; 2) I am familiar with a variety of technologies, data sources, and analytical methods (including a bit of statistics and machine learning); and 3) there wasn't anyone else who could help.

We quickly started evaluating different methods of estimating COVID-19 hospital admissions. The leaders brainstormed with other organizations in the region and discovered a few tools to evaluate. The first was a SIR model, which breaks up populations into three groups: Susceptible (S), Infected (I), and Removed (R). (Often R is "Recovered", but death is also a possibility; thus, "Removed" is more appropriate, although people could get reinfected.) This model shifts people between the three categories and assumes an upward trend, a single peak, then a downward trend. Graphs based on these models resemble bell curves. 

In order to tell this story, I have masked the data and simply labeled the volumes according to their subjective magnitude. The models all project hospital "census", meaning the number of beds that are in use each day, for COVID-19 patients. Here is the projection from Model 1. 

Model 1. SIR Model with Admissions, ICUs, and Ventilators

Model 1 foretold absolute disaster. The magnitude was many more times the available capacity. In essence, it did not matter what the y axis displayed: it was so large, no one would be able to handle the volume of hospital admissions. Model 1 assumed no interventions from anyone and was based on initial measurements of the reproductive number at about 3.2. The reproductive number can be interpreted as the number of people who become infected for every 1 person who already is infected. The first value of this number is the "basic reproductive number", R-naught, or R0; whereas subsequent numbers are called the "effective reproductive number", Re, or Rt.

Quickly, interventions began at many levels: national, state, and county. As a result, the initial model was no longer accurate. At this time, we still did not have actual admission data to compare with the models to assess accuracy, so we were still "flying blind".

Model 2, based on a logistic regression model fit to the Italian data, was much less dire. However, the model quickly doesn't make any sense, as the set of functions, called sigmoid functions, are monotonic functions - they never decrease (or increase if you flip it around). So the model was only good for the next couple of weeks. However, it gave us a more reasonable number to work with. We still didn't have actual data, but we did have bed capacity information.

Model 2. Logistic Model with Bed Capacity

Model 3, attempting to solve the problems with Model 2, was based on new studies from New York and other areas of the world, and was fit with a polynomial regression. Again, not a great model, but it did provide a more palatable near- and far-future state. The peaks of both Model 2 and Model 3 were very similar. We continued to compare to bed capacity.

Model 3. Polynomial Model with Bed Capacity

Model 4 was developed at about the same time as receiving actual hospital admissions data. Within 24 hours, I worked closely with an electronic medical record subject matter expert ("EMR SME", I suppose) and collected admissions, ICU stays, and ventilator usage for COVID-19 patients. Finally, we had actual data to compare with our models. 

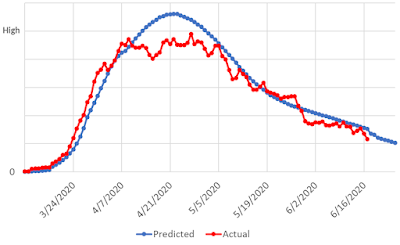Model 4. New SIR Model with Actual Hospitalizations

This model was another SIR model, based on a publicly available algorithm; however, unlike other SIR models, it incorporated changes in interventions by adjusting the reproductive number over time. Instead of assuming the number of cases would always increase at a flat rate, it spread the cases out based on the observed spread. Just like the prior SIR model, it suffered from modeling only one peak and monotonically descending from that peak. That is, it never increased again.

This worked very well for a few months. 

As the actual data and other public data sources demonstrated, cases can increase and decrease chaotically over time, based on the severity of interventions and whether people adhere to those interventions. It was possible that SARS-CoV-2 mutated, maybe a few times, and became more infectious as a result. In some regions we observed a "third peak", some of which were higher than the first, and at the time it wasn't done increasing, either.

Model 5 attempted to overcome the issues with SIR models, allowing for chaotic increases and decreases while still incorporating changes in the reproductive number. So far in this discussion, I have not explicitly named the models based on the sources from which they were based, for a variety of reasons. This model, though, is based on the LEMMA tool (Local Epidemic Modeling for Management & Action). Initially, this tool was built in R.

Model 5. LEMMA (R)

The LEMMA tool was "designed to provide regional... projections of the SARS-CoV-2 (COVID-19) epidemic under various scenarios" (from the tool's website). The model provided inputs for dates, population, observed cases (admissions, ICUs, and deaths), various parameters for PUI (patients under investigation) estimates, and more. It was incredibly flexible and, at the time, well-received.

At a certain point, the LEMMA developers decided to switch the foundation of the algorithm from the R-based models to a C++ package called Stan, which at its core is used for Bayesian statistics. As noted on the LEMMA website, "[The LEMMA] Stan implementation is based on the 'Santa Cruz County COVID-19 Model' (https://github.com/jpmattern/seir-covid19) by Jann Paul Mattern (UC Santa Cruz) and Mikala Caton (Santa Cruz County Health Services Agency)".

This model was a significant improvement, providing more intervention dates and input parameters. Model 6 was the last model, based on the LEMMA Stan package: 

Model 6. LEMMA (Stan)

In this variant of the model, we were able to extract the percentiles for the simulations and treat them as upper and lower estimates of the main prediction, specifically using the 95th and 5th percentiles, respectively. 

Note in the graphs, when comparing Model 5 and 6, that the two "bumps" in the early pandemic stages are more accurately modeled by Model 6. The first LEMMA model almost appeared as if there were two SIR models hiding underneath, with the maximum predicted values taken from each. Model 5 monotonically descended from the the first peak until a specific point where it changed direction. Model 6, on the other hand, had many changes of direction, leading to a more trusted result.

We ran this model once a week. Interventions, social behaviors, and the reproductive numbers changed rapidly within each of the geographic regions where we projected COVID-19 admissions, and as a result, we needed to continuously recalculate the model based on the latest information. 

Initially in Model 6, we guessed at the impact of various interventions in each region. At the same time, we were calculating the reproductive number in a separate process and reporting on it internally. My idea was to merge these two analyses in order to calculate the LEMMA model "intervention" percentage based on the actual observed reproductive number. I calculated the percent change from week to week and used that figure instead of guessing at the impact of various changes.

It wasn't perfect, but it worked rather well. I left the organization, and I heard from my former colleagues that the model continued to be used, and continued to take longer and longer to run. I suggested a few times that they simply cut off the model at a certain date and restart it, then merge the two results. Fortunately, by the time of this publication, it is no longer being used at all.

The models served their purpose - to provide foresight for planning and maybe a bit of fear, to help monitor, and to see the impact of interventions. Fortunately, we're out of the pandemic now (in my opinion). I post this now, finally, after having written it nearly two years ago, as a sort of professional horror story, a warning to others in the future, a reminder of what we need to do better.